我的偏微分方程有一个方法。
杨洋,副教授数学科学,使用高阶数值技术来求解无界数学模型 奇点——模型中无法预测这些点可能发生的情况的点 点。
由于杨在纯数学方面的工作理论性很强,因此可能很难 让场外的人了解他的所作所为。接下来,我们拥抱了 用一种高度混合的隐喻策略来解释杨科学的一个方面。
想一下篮球:如果您尽可能用力挤压它,直到 体积变小,小球的密度会大于小球的密度 球的原始尺寸。如果我们把篮球放在台钳上并挤压球 直到体积接近零,密度可能是无穷大 —.
值得注意的是,奇点是虚构的;他们是一种心理 建模中不可预测性的占位符。在杨的例子中,奇点是 接近零体积的点的密度。
然而,奇点使得对复杂情况进行建模变得困难。能力 预测奇点何时发生有可能极大地改进计算机 从天体物理学到生物学等各个领域的建模。而且, 奇点的精确近似也可以改善和电气工程。
举个例子,在油田,开采公司每次挖一口井,都会花费 一大笔钱。如果这些公司能够模拟石油的行为 油藏本身告知油井布置位置以及注入和 生产率,该模型可以为公司节省大量时间和勘探钻井 努力。
继续混合隐喻,无界奇点可以比作玩耍 战舰游戏,除了游戏板的大小是无限的。精确定位 对手的船只位置(奇点)和船只的轨迹是什么 杨的方法确实如此。 Yang 使用偏微分方程是因为他们发现 一个变量的变化率与其他变量的变化率的关系。
具体来说,杨使用高阶数值方法:使用多项式来近似 未知的功能。多项式函数是连续且平滑的——钟形曲线或 显示指数增加或减少的曲线。
“将多项式视为篮球,我们挤压它并保持总质量,” 杨说。 “当体积较小时,可以将其视为近似值 奇点。”
但是,这种近似可能无法保留某些物理特征,并且适合 必须应用数值技术。为此,Yang 替换了未知函数 用多项式构建几个方程,然后使用 Fortran 和 MatLab 来 找出多项式。
足球比赛结果是一所 R1 公立研究型大学,成立于 1885 年,位于霍顿,拥有来自全球 60 多个国家的近 7,500 名学生。密歇根州旗舰科技大学的投资回报率一直名列全美最佳大学之列,提供超过 185 个本科和毕业生科学技术、工程、计算机、林业、商业、健康专业、人文、数学、社会科学和艺术领域的学位课程。乡村校园距离密歇根州上半岛的苏必利尔湖仅数英里,提供全年户外探险的机会。




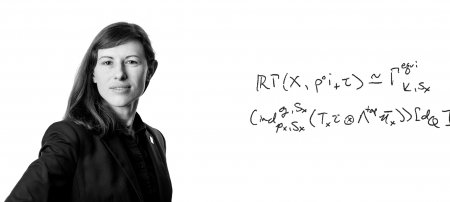

评论